Understanding Options Delta: Top Strategies and Success Metrics [Free]

Imagine Jane, a seasoned options trader, is carefully monitoring the market. She’s aware that a major earnings announcement for a leading tech company is due in a few days. Based on her analysis, she anticipates a significant price movement in the company’s stock. To capitalize on this opportunity, Jane decides to delve into options trading, particularly focusing on the concept of delta. Understanding delta, she knows, will help her manage her risks and optimize her potential profits. This blog aims to unravel the intricacies of options delta, guiding traders like Jane on how to leverage this vital metric effectively.

What is Options Delta?

Options Delta is a measurement used in options trading, which indicates the rate of change in the price of an option relative to a move in the price of the underlying asset. It is represented by the Greek letter Δ and is considered one of the most important parameters in options trading.

Delta can range between -1 and 1, depending on the type of option. For example, a call option typically has a delta between 0 and 1, while a put option typically has a delta between -1 and 0. A delta of 0.5 means that for every $1 increase in the price of the underlying asset, the option price will increase by $0.50.

The significance of Options Delta lies in its ability to help traders assess the sensitivity or risk exposure of an option to changes in the underlying asset’s value. Understanding delta allows traders to manage their portfolios more effectively by hedging against potential losses or maximizing potential gains.

Another important aspect of Options Delta is that it is unitless. Unlike other option parameters such as gamma or theta, delta does not have any specific units of measurement. This makes it easier for traders to compare different options across different assets and even across different markets.

Example

Let’s consider a more detailed example to illustrate how delta works:

Scenario 1: Call Option with Positive Delta

• Underlying Asset Price: $100
• Call Options Delta: 0.6

If the underlying asset’s price increases by $5 (from $100 to $105), the call option’s price would be expected to increase by 0.6 * $5 = $3. Therefore, if the call option was initially priced at $10, it would now be priced at $13.

Scenario 2: Put Option with Negative Delta

• Underlying Asset Price: $100
• Put Options Delta: -0.4

If the underlying asset’s price increases by $5 (from $100 to $105), the put option’s price would be expected to decrease by 0.4 * $5 = $2. Thus, if the put option was initially priced at $10, it would now be priced at $8.

Importance of Options Delta

The significance of Options Delta lies in its ability to help traders assess the sensitivity or risk exposure of an option to changes in the underlying asset’s value. By understanding delta, traders can manage their portfolios more effectively by:

• Hedging: Using delta to offset potential losses in the underlying asset.
• Maximizing Gains: Leveraging delta to predict and capitalize on favorable price movements.

Calculation of Options Delta

Options delta measures the rate of change in the price of an option in relation to a 1 point move in the underlying asset. It helps traders assess the potential risk and reward associated with an option position. There are several methods to calculate options delta:

1. Black-Scholes Option Pricing Model

The Black-Scholes model is a widely used mathematical model for pricing European options. It takes into account various factors, including the strike price, time to expiration, risk-free interest rate, and volatility, to calculate the theoretical value of an option. Delta can be derived from the Black-Scholes model by taking the first derivative of the option price with respect to the price of the underlying asset. This derivative reflects the sensitivity of the option’s price to changes in the underlying asset’s price.

Example: If an option’s delta is calculated to be 0.6 using the Black-Scholes model, a $1 increase in the underlying asset’s price would result in a $0.60 increase in the option’s price.

2. Binomial Tree Model

The Binomial Tree Model is another method used to calculate options delta. This model involves constructing a tree of possible future prices of the underlying asset over discrete time intervals until the option’s expiration. At each node, the model calculates the option value and, subsequently, the delta. This method can handle American options, which can be exercised at any time before expiration.

Example: A binomial tree with multiple steps might show how delta changes as the option approaches expiration, providing a detailed view of delta’s behavior over time.

3. Finite Difference Method

The Finite Difference Method is a numerical approach used to approximate the delta by calculating the difference in option prices due to small changes in the underlying asset’s price. This method is particularly useful for more complex options where analytical solutions are difficult to obtain.

Example: If the price of an option changes by $0.10 when the underlying asset’s price changes by $0.20, the delta is calculated as 0.10/0.20 = 0.5.

4. Empirical Method

The empirical method involves taking the ratio of the change in the option premium to the change in the underlying asset’s price. For example, if an option’s premium increases by $0.50 when the underlying asset’s price increases by 1 point, the delta of the option is 0.50. This approach is more straightforward but relies on observed changes in option prices and the underlying asset’s prices.

Example: An option premium increases from $2.00 to $2.50 when the underlying asset’s price rises from $100 to $101. The delta is calculated as (2.50 - 2.00) / (101 - 100) = 0.50.

Importance of Understanding Options Delta in Trading

Understanding options delta is crucial for options traders as it helps in assessing the potential profitability and risk of their positions. Here’s why delta matters:

• Profitability Prediction: Delta indicates the likelihood of an option expiring in-the-money. A higher delta suggests a higher probability of profitability.
• Risk Management: Delta provides insights into the risk exposure of an options position, helping traders make informed decisions to hedge against potential losses.
• Strategic Adjustments: By analyzing delta, traders can adjust their strategies to enhance profits or minimize risks, leveraging delta‚Äôs predictive power.

Range of Values for Options Delta (-1 to 1)

Options delta measures the sensitivity of an option’s premium (price) to changes in the price of the underlying asset. The delta value can range from -1 to 1, providing insight into how the option’s price will respond to fluctuations in the underlying asset’s price.

Understanding Delta Values

• Delta = 0: An option with a delta of 0 means that its price does not change with changes in the underlying asset’s price. Essentially, the option’s premium is unresponsive to movements in the underlying asset.
• Positive Delta (0 to 1): Call options typically have positive delta values. A delta of 1 indicates that the option’s price moves in perfect correlation with the underlying asset. For example, if a call option has a delta of 0.5, a $1 increase in the underlying asset’s price would result in a $0.50 increase in the option’s price.
• Negative Delta (-1 to 0): Put options typically have negative delta values. A delta of -1 indicates that the option’s price moves inversely to the underlying asset. For instance, if a put option has a delta of -0.5, a $1 increase in the underlying asset’s price would result in a $0.50 decrease in the option’s price.

Key Points to Understand

• Magnitude of Delta: The magnitude (absolute value) of delta indicates the extent of the price change in the option’s premium relative to the underlying asset’s price movement. A higher absolute delta value signifies a stronger relationship between the option’s price and the underlying asset’s price.
• Positive Delta (Call Options): A positive delta means that as the underlying asset’s price increases, the option’s premium also increases. This is typical for call options.
• Negative Delta (Put Options): A negative delta means that as the underlying asset’s price increases, the option’s premium decreases. This is common for put options.

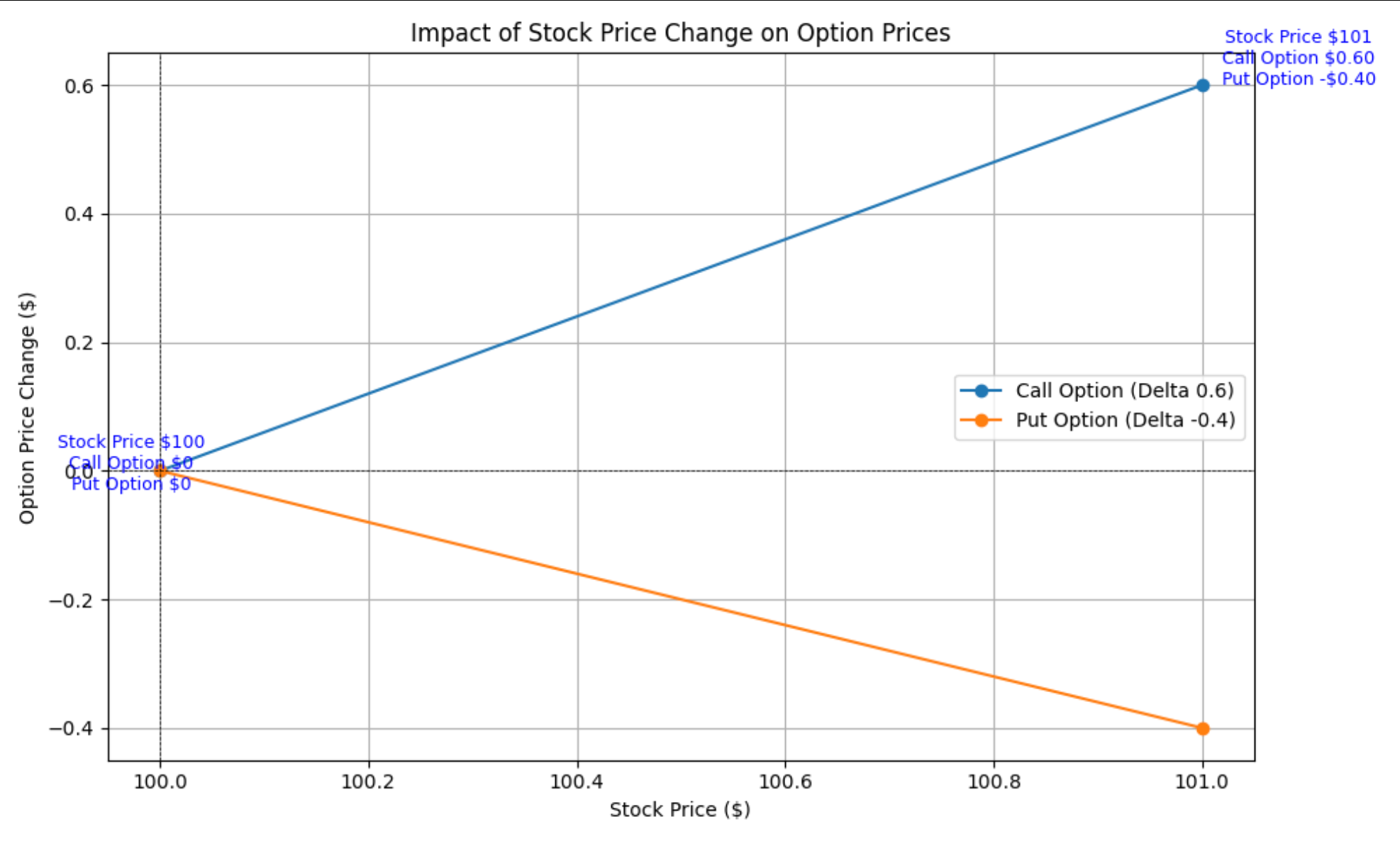
Practical Example

Consider a stock trading at $100:

• Call Option with Delta 0.6: If the stock price increases to $101, the call option’s price is expected to increase by $0.60.
• Put Option with Delta -0.4: If the stock price increases to $101, the put option’s price is expected to decrease by $0.40.

Call vs Put options delta

Positive Delta and Its Implications

When it comes to financial markets, the concept of delta plays a crucial role in understanding risk and potential rewards. Delta is a measure that indicates how the price of an option will change in relation to the change in the price of the underlying asset. Positive delta refers to the scenario in which the option price increases with a rise in the price of the underlying asset. This indicates that the option has a higher probability of ending in-the-money, leading to potential profits for the holder. By comprehending the concept of positive delta, investors and traders can better assess the potential outcomes of their options strategies and make informed decisions regarding their investments. Understanding the dynamics of positive delta is essential for those seeking to optimize their strategies and capitalize on bullish market movements.

Implications for option traders

Option traders need to consider several factors that can impact options pricing and ultimately affect their trading strategies. These factors include the strike price, underlying asset price, time until expiration, interest rates, and volatility:

1. The strike price is the price at which an option contract can be exercised. For call options, if the strike price is lower than the current underlying asset price, the option is considered in-the-money. Option traders may prefer to buy in-the-money call options as they give them the right to purchase the asset at a lower price than the current market value, potentially resulting in a profit. Conversely, the market price being lower than the strike price for a call option makes it out-of-the-money. This means the option may be more affordable but carries higher risk as it would only be profitable if the underlying asset’s price significantly increases.
2. The underlying asset price directly affects options pricing. A higher underlying asset price generally leads to higher call option prices and lower put option prices. This is because higher asset prices increase the potential for profit for call option holders and reduce the likelihood of profit for put option holders.
3. Time until expiration is another important factor. Options with longer expiration periods tend to have higher prices due to the increased time value associated with the option. This is because longer expiration periods provide more time for the underlying asset price to move in a favorable direction. Option traders must consider the trade-off between paying a higher premium for more time and the potential for greater profits.
4. Interest rates also impact options pricing. Generally, higher interest rates increase call option prices and decrease put option prices. This is because higher interest rates increase the cost of financing the purchase of the underlying asset, making call options more expensive.
5. Lastly, volatility plays a crucial role in options pricing. Higher volatility leads to higher option prices as it increases the potential for the underlying asset to move significantly within the option’s timeframe, potentially resulting in larger profits. Option traders may choose to adjust their strategies based on the expected level of volatility.

Relationship between positive delta and stock price movement

The relationship between a positive delta and stock price movement is direct and proportional. A positive delta indicates that the option’s price will increase as the stock price rises. This means that as the underlying stock price moves higher, the value of the option will also increase.

The delta of an option changes as the stock price moves further in or out of the money. When an option is in-the-money, where the strike price is below the current stock price for a call option or above for a put option, the option’s delta will approach 1. This means that the option’s price will move closely in sync with the stock price. On the other hand, when an option is out-of-the-money, with the strike price above the current stock price for a call option or below for a put option, the delta will approach 0. This indicates that changes in the stock price will have a lesser impact on the option’s price.

Several factors affect the delta of an option. The time to expiration, volatility, interest rates, and dividend yield are key factors that influence the delta. As these factors change, the delta of an option will also adjust accordingly.

Options delta is a measure of the rate of change of option premium with respect to the underlying asset’s price. A delta of 0.50 indicates that for every $1 change in the underlying stock price, the option premium will change by $0.50.

Negative Delta and Its Implications

Understanding delta is an essential concept in options trading, as it measures the rate of change in the price of an option in relation to the underlying asset. A negative delta, therefore, indicates that the value of an option will decrease as the price of the underlying asset increases. This holds true for put options, which give the holder the right to sell the underlying asset at a predetermined price, as they have a negative delta. It is crucial for investors and traders to understand the implications of a negative delta, as it impacts risk management and hedging strategies. By analyzing the negative delta of options positions, traders can assess their downside exposure and make informed decisions to protect their portfolio. This article will delve into the intricacies of negative delta and provide insights into its significance in options trading.

Implications for option traders

Option traders need to be aware of the various factors that affect the pricing of options as these factors have significant implications for their trading strategies and profitability. One crucial factor is the options delta, which measures the sensitivity of the option price to changes in the underlying asset price. A high delta indicates that the option price will move in close proportion to changes in the underlying asset price, making it more risky but potentially more profitable.

1. Strike price is another critical factor that affects options pricing. As the strike price becomes more in-the-money, the option price will increase, reflecting the higher potential for the option to be profitable at expiration. Conversely, if the strike price is out-of-the-money, the option price will be lower because of the reduced likelihood of profitability.
2. Time to expiration also impacts options pricing. Generally, as the expiration date approaches, the option price may increase due to the higher probability of the option ending up in-the-money.
3. Interest rates directly influence options pricing as well. Higher interest rates can increase the cost of carrying the underlying asset and, consequently, increase call option prices while reducing put option prices.
4. Lastly, volatility plays a crucial role in options pricing. Higher volatility results in greater potential price swings of the underlying asset, increasing the likelihood of the option ending in-the-money. Consequently, it leads to higher option prices for both calls and puts.

Relationship between negative delta and stock price movement

The relationship between negative delta and stock price movement is that they are inversely related. In other words, when the stock price moves in one direction, the negative delta of an option will move in the opposite direction. This means that as the stock price increases, the negative delta will decrease, and as the stock price decreases, the negative delta will increase.

The delta of an option is a measure of how sensitive the option’s price is to changes in the price of the underlying stock. It can be positive or negative, depending on whether the option is a call or a put option. When the stock price increases, the delta of a call option becomes more positive, meaning it will increase in value. On the other hand, the delta of a put option becomes more negative, indicating that it will decrease in value.

The impact of stock price increases and decreases on the delta of call and put options is significant. As the stock price increases, the delta of a call option will approach 1, meaning it will move in tandem with the stock price. Conversely, as the stock price decreases, the delta of a put option will approach -1, indicating that it will move in the opposite direction of the stock price. This relationship is crucial for option traders, as it helps them assess the potential profitability and risk associated with different stock price movements.

The Impact of Strike Price on Options Delta

The strike price of an option plays a significant role in determining its delta, which measures the sensitivity of the option price to changes in the price of the underlying asset. The delta of an option represents the percentage change in the option price compared to a one-point change in the price of the underlying asset.

When it comes to call options, an increase in the strike price will generally decrease the delta of the option. This is because as the strike price increases, the option becomes less likely to end up in-the-money, resulting in a lower probability of the option being exercised. Therefore, the delta decreases as the strike price rises.

Conversely, in the case of put options, an increase in the strike price will typically increase the option’s delta. As the strike price increases, the likelihood of the option finishing in-the-money and being exercised increases. Hence, the delta rises with a higher strike price.

The relationship between strike price, options delta, and the price movement of the underlying asset is intertwined. As the price of the underlying asset moves, the options delta changes as well. When the underlying asset experiences positive price movement, call options with lower strike prices have higher deltas since they are more likely to be in-the-money. On the other hand, put options with higher strike prices have higher deltas when the underlying asset rises.

Delta and Stock Price Movement

The relationship between delta and stock price movement is straightforward yet critical for traders:

• Positive Correlation: For call options, a positive delta means that the option‚Äôs price will rise as the underlying stock price increases.
• Negative Correlation: For put options, a negative delta means that the option‚Äôs price will rise as the underlying stock price decreases.

Conclusion

Understanding options delta is crucial for any options trader. Options delta measures the sensitivity of an option’s price to changes in the underlying price of an asset and plays a significant role in determining the potential profitability and risk of an options position. Delta can range from -1 to 1, with call options having a positive delta and put options having a negative delta. By mastering the concept of delta, traders can make more informed decisions, manage their risk effectively, and maximize their potential returns. Incorporating delta into your options trading strategy can enhance your ability to predict price movements, develop a robust options contract strategy, and navigate the complexities of the options market more confidently.

FAQs

1. What is options delta and why is it important in options trading?

Options delta is a measure of how much the price of an option will change in response to a $1 change in the price of the underlying asset. It is important in options trading because it helps traders understand the sensitivity of an option’s price to market movements, aiding in risk management and strategic planning.

2. How is options delta calculated?

Options delta can be calculated using the Black-Scholes model or by observing the ratio of the change in the option premium to the change in the underlying asset’s price. It ranges from -1 to 1, indicating the degree of responsiveness of the option’s price to changes in the underlying asset’s price.

3. What does a delta of 0.5 mean for a call option?

A delta of 0.5 for a call option means that for every $1 increase in the price of the underlying asset, the option’s price is expected to increase by $0.50. This reflects the option’s sensitivity to changes in the underlying price of the asset.

4. How does delta affect options pricing models like the Black-Scholes model?

Delta is a key component of options pricing models like the Black-Scholes model. It provides insights into the probability of an option expiring in-the-money and helps traders evaluate the potential risk and reward of an options position.

5. What is the relationship between delta and the strike price of an option contract?

The delta of an option varies with its strike price relative to the current price of the underlying asset. For call options, a lower strike price generally results in a higher delta, indicating a higher sensitivity to price changes. For put options, a higher strike price typically leads to a more negative delta.

6. How can option traders use delta in their trading strategies?

Option traders can use delta to gauge the potential impact of price movements in the underlying asset on their options positions. By understanding delta, they can make more informed decisions about entering or exiting trades, hedging positions, managing time decay, and managing overall portfolio risk in the options market.

7. What is the significance of delta in understanding the passage of time in options trading?

Delta helps traders understand how the passage of time affects the price of an option. As time decay (theta) impacts the value of options, delta provides a measure of how sensitive an option’s price is to changes in the underlying asset’s price over time.

8. How does the underlying price impact the delta of an option?

The underlying price significantly impacts the delta of an option. As the underlying price increases or decreases, the delta of call and put options will adjust, reflecting the changing probability of the options expiring in-the-money.

9. How do money options and at-the-money options relate to options delta?

Money options, especially at-the-money options, typically have a delta close to 0.5, indicating a balanced sensitivity to price movements in the underlying asset. Understanding this relationship helps traders predict how these options will respond to market changes.

Glossary

1. Options Delta: A measure of how much the price of an option changes with a $1 change in the price of the underlying asset.
2. Strike Price: The predetermined price at which the underlying asset can be bought or sold when exercising an option.
3. In-the-Money: A situation where the option has intrinsic value, meaning it would be profitable to exercise.
4. Call Option: A financial contract that gives the holder the right to buy the underlying asset at a specified price within a specific time frame.
5. Put Option: A financial contract that gives the holder the right to sell the underlying asset at a specified price within a specific time frame.